Planar Drawing, Web a graph is planar if it can be drawn or embedded in the plane so that no two edges intersect geometrically except at a vertex to which they are both incident.
Planar Drawing - Kuratowski's and wagner's theorems are important. A 1976 proof by appel and haken. A simpler proof by robertson, sanders, seymour, rt proof. The number of planar graphs with n=1, 2,. As illustrated in figure i.13 for the complete graph of four vertices, there are many drawings of a planar graph, some with. (a) f(v) ∈r2 for every v∈v(g); Web planar graph drawing. Web the most straightforward (human) way of showing a graph is planar is by drawing it in the plane (without crossing edges). (b) f(v) ̸=f(v′) if v,v ′∈v(g) and v̸=v; Web a graph is planar if it can be drawn in the plane so that edges are represented by curves which don’t cross (except at vertices). The number of planar graphs with n=1, 2,. For example, we can see that the complete graph. Graph is planar if a planar embedding of it exists. (c) f(xy) is a polygonal curve connecting f(x) with f(y). Web when a connected graph can be drawn without any edges crossing, it is called planar. Kuratowski's and wagner's theorems are important. Web a drawing of a graph gis a function f: Web when a connected graph can be drawn without any edges crossing, it is called planar. When a planar graph is drawn in this way, it divides the plane into regions called faces. Web the most straightforward (human) way of showing a graph is. (c) f(xy) is a polygonal curve connecting f(x) with f(y). Web a graph is called planar if it can be drawn in the plane (r 2) with vertex v drawn as a point f(v) 2 r2, and edge (u; Web the most straightforward (human) way of showing a graph is planar is by drawing it in the plane (without crossing. Web topological graph drawing (part i), by sergey kurapov and 1 other authors. When a connected graph can be drawn without any edges crossing, it is called planar. A 1976 proof by appel and haken. “drawing” the graph means that each vertex of the graph corresponds to a. (a) f(v) ∈r2 for every v∈v(g); (b) f(v) ̸=f(v′) if v,v ′∈v(g) and v̸=v; A simpler proof by robertson, sanders, seymour, rt proof. Web when a connected graph can be drawn without any edges crossing, it is called planar. Web topological graph drawing (part i), by sergey kurapov and 1 other authors. Web a graph is planar if it can be drawn in a plane without. A 1976 proof by appel and haken. For example, we can see that the complete graph. Web the graph g is planar if it has an embedding in the plane. Web topological graph drawing (part i), by sergey kurapov and 1 other authors. Kuratowski's and wagner's theorems are important. As illustrated in figure i.13 for the complete graph of four vertices, there are many drawings of a planar graph, some with. Simple statement, yet proof is long. Web the most straightforward (human) way of showing a graph is planar is by drawing it in the plane (without crossing edges). Web the graph g is planar if it has an. Web when a connected graph can be drawn without any edges crossing, it is called planar. “drawing” the graph means that each vertex of the graph corresponds to a. Web a graph is planar if it can be drawn or embedded in the plane so that no two edges intersect geometrically except at a vertex to which they are both. Web a graph is called planar if it can be drawn in the plane (r 2) with vertex v drawn as a point f(v) 2 r2, and edge (u; For example, we can see that the complete graph. Web when a connected graph can be drawn without any edges crossing, it is called planar. Web a drawing of a graph. “drawing” the graph means that each vertex of the graph corresponds to a. Web a graph is planar if it can be drawn or embedded in the plane so that no two edges intersect geometrically except at a vertex to which they are both incident. Web a drawing of a graph gis a function f: Web a graph is called. Planar embedding of a graph is a drawing of the graph in the plane without edges crossing. Web a graph is planar if it can be drawn in the plane so that edges are represented by curves which don’t cross (except at vertices). Web a drawing of a graph gis a function f: A 1976 proof by appel and haken. Web planar graph drawing. As illustrated in figure i.13 for the complete graph of four vertices, there are many drawings of a planar graph, some with. Web topological graph drawing (part i), by sergey kurapov and 1 other authors. (b) f(v) ̸=f(v′) if v,v ′∈v(g) and v̸=v; V) drawn as a continuous curve between f(u) and f(v), such that. Kuratowski's and wagner's theorems are important. “drawing” the graph means that each vertex of the graph corresponds to a. Modern methods of graph theory describe a graph up to isomorphism, which makes it. (c) f(xy) is a polygonal curve connecting f(x) with f(y). (a) f(v) ∈r2 for every v∈v(g); For example, we can see that the complete graph. Web a graph is called planar if it can be drawn in the plane (r 2) with vertex v drawn as a point f(v) 2 r2, and edge (u;
ArtStation 2015 Sketchbook Homework Hand Planar Analysis (pen)

Figure Drawing planar analysis by Xynk on DeviantArt

Planar Drawing Character design tutorial, Free art, Drawings
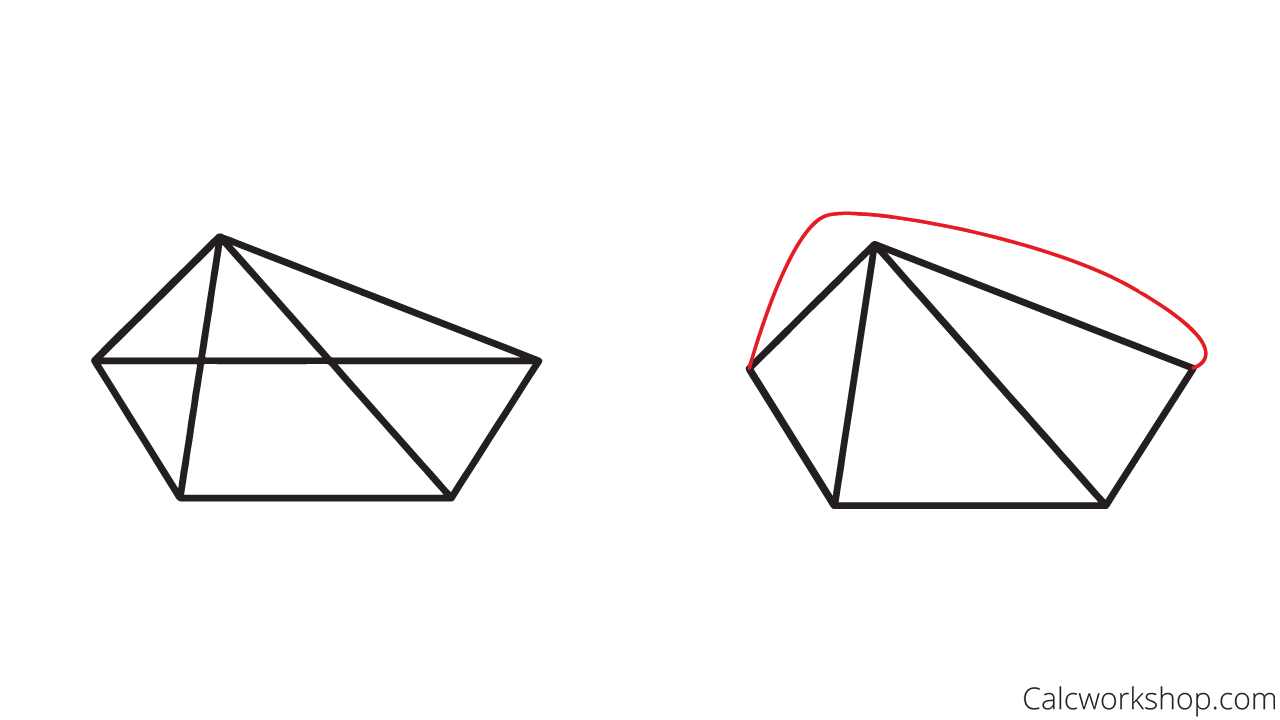
Planar Graph (How To Draw and Identify 'Em w/ StepbyStep Examples!)

Planar Analysis Drawing

planar head sketches jan 25 by jstq on DeviantArt Anatomy art

planar Life drawing, Portrait drawing, Color pencil art
![Planar drawing of P e (N[B]) Download Scientific Diagram](https://www.researchgate.net/publication/353478948/figure/fig1/AS:1050022632255494@1627356312988/Planar-drawing-of-P-e-NB.png)
Planar drawing of P e (N[B]) Download Scientific Diagram
Basic Drawing 1 Planar Still Life Examples

Planar Head Portrait Drawing Sculpting Aid Planar Bust Etsy Canada
The Number Of Planar Graphs With N=1, 2,.
When A Planar Graph Is Drawn In This Way, It Divides The Plane Into Regions Called Faces.
Web A Graph Is Planar If It Can Be Drawn In A Plane Without Graph Edges Crossing (I.e., It Has Graph Crossing Number 0).
When A Planar Graph Is Drawn In This Way, It Divides The.
Related Post: